Taks 6 "Aljabar Boolean, Penyederhanaan Logika, dan Peta Karnaugh"

 Standar Form of Boolean Expressions, Contains:

1. The Sums of Product (SOP) Form

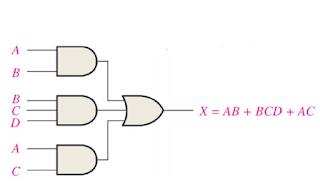
When two or more product terms are summed by Boolean addition

AB + ABC

ABC + CDE + BC+ D

2. The Product of Sum 

When two or more sum terms are multiplied.

                           (A + B )(A + B+ C )

                           ( A + B )( A + B + C ) (A + C )

The Karnaugh Map

- Provides a systematic method for simplifying Boolean expressions 

-Produces the simplest SOP or POS expression 

- Similar to a truth table because it presents all of the possible values of input variable

K-map Simplification of  SOP Expressions

-A group must contain either 1, 2, 4, 8 or 16 cells. 

-Each cell in group must be adjacent to one or more cells in that same group but all cells in the group do not have to be adjacent to each other 

-Always include the largest possible number 1s in a group in accordance with rule 1 

-Each 1 on the map must be included in at least one group. 

The 1s already in a group can be included in another group as long as the overlapping groups include noncommon 1s.

Determining Minimum SOP Expressions of the map

Groups the cells that have 1s. Each group of cells containing 1s create one product term composed of all variables that occur in only one form (either uncomplemented or complemented) within the group. Variable that occurs both uncomplemented and complemented within the group are eliminated. These are called contradictory variables. 

Sumber : Klik disini